Finite-element discretizations come along with different options in order to define a coupling interface. Given a common (here fourth-order) finite element, we have:
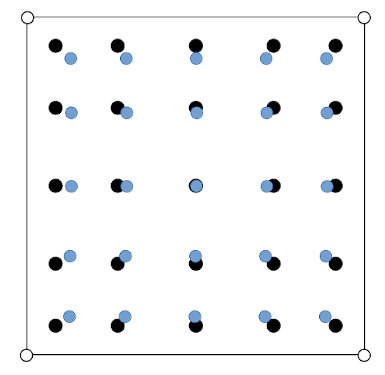
- geometry-based interfaces such as vertices (black, circular contour) at the element corners or the face centers,
- the finite-element support points (black, filled circles) and
- the quadrature points (blue, filled circles).
Geometry-based interfaces
Using the geometry in order to define a coupling interface seems like one of the most obvious choices, since the coordinate information is usually easy to access. The major drawback is, however, that the resolution of the coupling interface is independent of the discretization and you might lose information across the coupling interface. Considering our example element above, a coupling mesh based on geometric vertices would consist of four interface nodes, whereas the other choices have considerably more (25) interface nodes. The overall difference between the geometry-based interface and both other options is related to the polynomial degree of the finite-element support points (assuming a polynomial FE basis for the moment). In case the code you want to couple uses solely linear elements, the resulting number of interface nodes coincide with the vertex based coupling mesh and the element vertices might be a perfect choice for your application case. For an increasing polynomial degree, geometry-based interfaces become less attractive.
In addition to the resolution of the coupling interface, another challenge in this context is given by the required solution transfer between the FE solution space and the geometric quantity used for coupling purposes. One has to average over an element face or map the solution within the solver to the vertex location.
Support points
Finite-element support points are based on the finite-element discretization. Not all finite-element discretizations have support points, e.g., Legendre finite elements based on a modal decomposition have none. However, we focus here on polynomial finite elements with support points, which are a common choice in many applications. The major advantage of support points is that the solution values live typically on the support points and the values can be passed easily to preCICE by reading them from the solution vector. Also, increasing the polynomial degree of the discretization increases the number of coupling interface nodes in contrast to the geometry based coupling interface.
However, this approach runs into trouble in case the support points live on element faces in a discontinuous solution space (discontinuous Galerkin approach), since you define interface nodes multiple times. In particular, the duplicate definition becomes problematic if an interpolant is constructed from the coupling mesh in preCICE, which happens for the from mesh in a read-consistent setup and for the to mesh in a write-conservative setup (see also the mapping configuration).
Another issue using higher-order support points might appear in case you run very large cases and strive for the RBF mapping of preCICE. In case the support points are non-equally distributed within the element (shown in our example element above and as it is usually the case in order to preserve a reasonable conditioning of other system matrices), the RBF mapping becomes ill-conditioned due to the varying distance of interface nodes all over the place. Have a look at the paper “Radial basis function interpolation for black-box multi-physics simulations” for detailed information. Again, this issue is only relevant if the RBF interpolant is constructed from the non-equally distributed FEM mesh (see the section above for the related mapping configuration).
Quadrature points
Quadrature points refer to the points used for numerical quadrature when assembling the matrices of the finite-element system. The location of the quadrature points depend on the employed quadrature formula, where the Gauss-Legendre quadrature is by far the most common choice. Still, there are good reasons to select a different quadrature formula. Using the Gauss-Legendre quadrature points comes in the first place with the same issue of potentially ill-conditioned RBF mappings as described in the section above. However, reading data at the quadrature point location removes the additional mapping from the support point location to the quadrature points, which is usually executed by your solver.
Conclusion
There are various options how to deal with FEM meshes in preCICE and the best choice depends on the solver you want to couple. In many FEM solvers, the desired write data location is typically related to the support points and the desired read data location is typically related to the quadrature points, since the data is computed/required in these locations. Therefore, you might even consider to define different meshes for reading data from and writing data to preCICE.
In case the data location can be chosen independent of the problem setup, e.g., you can sample the solution at arbitrary points, you might also consider to create an equally-distributed interface mesh. Due to the equally distributed nodes, a well-conditioned RBF mapping can be retained (see the section above about the ill-conditioning). In addition, you could compensate the limited convergence order of the mapping algorithms to some extent by increasing the number of interface nodes artificially, if you use higher-order schemes on your finite-element participant.