Setup
We solve a partitioned heat equation. For information on the non-partitioned case, please refer to [1, p.37ff]. In this tutorial the computational domain is partitioned and coupled via preCICE. The coupling roughly follows the approach described in [2].
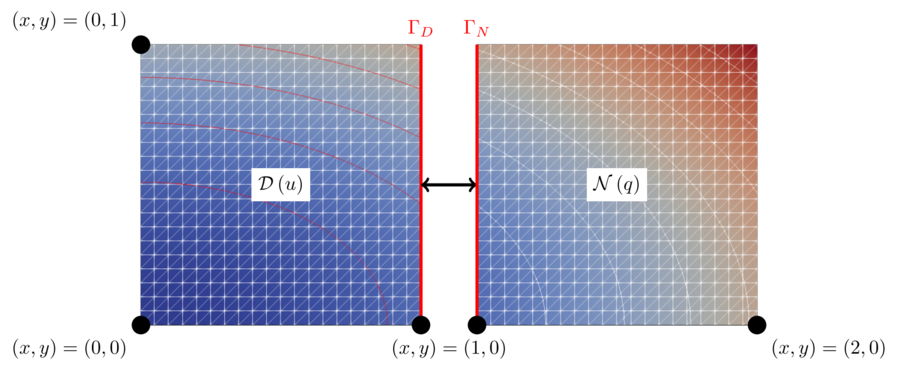
Case setup from [3]. D denotes the Dirichlet participant and N denotes the Neumann participant.
The heat equation is solved on a rectangular domain Omega = [0,2] x [0,1] with given Dirichlet boundary conditions. We split the domain at x_c = 1 using a straight vertical line, the coupling interface. The left part of the domain will be referred to as the Dirichlet partition and the right part as the Neumann partition. To couple the two participants we use Dirichlet-Neumann coupling. Here, the Dirichlet participant receives Dirichlet boundary conditions (Temperature) at the coupling interface and solves the heat equation using these boundary conditions on the left part of the domain. Then the Dirichlet participant computes the resulting heat flux (Flux) from the solution and sends it to the Neumann participant. The Neumann participant uses the flux as a Neumann boundary condition to solve the heat equation on the right part of the domain. We then extract the temperature from the solution and send it back to the Dirichlet participant. This establishes the coupling between the two participants.
This simple case allows us to compare the solution for the partitioned case to a known analytical solution (method of manufactures solutions, see [1, p.37ff]). For more usage examples and details, please refer to [3, sect. 4.1].
Configuration
preCICE configuration (image generated using the precice-config-visualizer):
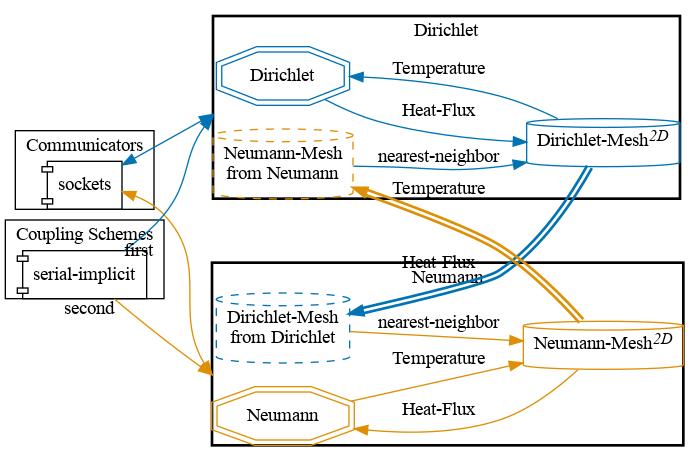
Available solvers and dependencies
You can either couple a solver with itself or different solvers with each other. In any case you will need to have preCICE and the python bindings installed on your system.
-
FEniCS. Install FEniCS and the FEniCS-adapter. The code is largely based on this fenics-tutorial from [1].
-
Nutils. Install Nutils.
-
OpenFOAM. This case uses the custom heatTransfer solver (find it in
solver-openfoamand build withwmake). Read more details in the OpenFOAM adapter.
Running the simulation
You can find the corresponding run.sh script for running the case in the folders corresponding to the solver you want to use.
For choosing whether you want to run the Dirichlet-kind and a Neumann-kind participant, please provide the following commandline input:
-dflag will enforce Dirichlet boundary conditions on the coupling interface.-nflag will enforce Neumann boundary conditions on the coupling interface.
For running the case, open two terminals run:
cd fenics
./run.sh -d
and
cd fenics
./run.sh -n
If you want to use Nutils, use cd nutils instead of cd fenics. The FEniCS case also supports parallel runs. Here, you cannot use the run.sh script, but must simply execute
mpirun -n <N_PROC> heat.py -d
Note on the combination of Nutils & FEniCS
You can mix the Nutils and FEniCS solver, if you like. Note that the error for a pure FEniCS simulation is lower than for a mixed one. We did not yet study the origin of this error, but assume that this is due to the fact that Nutils uses Gauss points as coupling mesh and therefore entails extrapolation in the data mapping at the top and bottom corners.
Visualization
Output is written into the folders fenics/out and nutils.
For FEniCS you can visualize the content with paraview by opening the *.pvd files. The files Dirichlet.pvd and Neumann.pvd correspond to the numerical solution of the Dirichlet, respectively Neumann, problem, while the files with the prefix ref correspond to the analytical reference solution, the files with error show the error and the files with ranks the ranks of the solvers (if executed in parallel).
For Nutils, please use the files Dirichlet-*.vtk or Neumann-*.vtk. Please note that these files contain the temperature as well as the reference solution.

Visualization in paraview for x_c = 1.5.
References
[1] Hans Petter Langtangen and Anders Logg. “Solving PDEs in Minutes-The FEniCS Tutorial Volume I.” (2016). pdf
[2] Azahar Monge and Philipp Birken. “Convergence Analysis of the Dirichlet-Neumann Iteration for Finite Element Discretizations.” (2016). Proceedings in Applied Mathematics and Mechanics. doi
[3] Benjamin Rüth, Benjamin Uekermann, Miriam Mehl, Philipp Birken, Azahar Monge, and Hans Joachim Bungartz. “Quasi-Newton waveform iteration for partitioned surface-coupled multiphysics applications.” (2020). International Journal for Numerical Methods in Engineering. doi